Month: April 2018

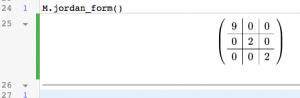
This week, the main new computational topic is complex eigenvalues and eigenvectors. Sage finds complex eigenvalues / eigenvectors by default, so we already know how to find complex eigenvectors:
A = matrix([[1,-2],[1,3]])
A.eigenvalues()
A.eigenvectors_right()

Note that Sage uses “I” to stand for i, the square root of -1. (This choice is because “i” is often used as an index, as in “for i=1…5”.) Manipulations work as you would expect:
I^2
z=2+3*I
z
z^2
z+z

Sometimes you want to extract the real part or the imaginary part of a complex number:

z
z.real()
z.imag()

The norm of a complex number a+bi is sqrt(a^2+b^2). Sage (reasonably) calls this the “absolute value”:
z.abs()

The complex conjugate of a+bi is a-bi.
z.conjugate()

We can check some identities, like:
bool(z.abs() == sqrt(z*z.conjugate())
bool(z.real() == (z+z.conjugate())/2)

(The “bool” means we want to know if the expression is true or false, i.e., we want a “boolean“.)

Some things work the same for vectors:
v=vector([1+I,2+3*I])
v.conjugate()
v.real()
Hmm… v.real() didn’t work. We can get around this by using the identity above:

(v+v.conjugate())/2

Another way is to use a bit more Python:
vector([x.real() for x in v])

You can also use exponential (or polar) notation for complex numbers. Use exp(x) for e^x. So:

exp(pi*i)
exp(2*pi*I)
4*exp(pi*I/4)

If we want to convert rectangular representations of complex number to polar ones, we already know how to get the length, with z.abs().  The angle is the argument, so use arg(z). (Why this isn’t z.arg() is a mystery to me.)

arg(z)
arg(i)
arg(1+I)
arg(1+sqrt(3)*I)

As you’ll notice, Sage is remarkably bad at doing this symbolically: it just sort of throws up its hands at 1+sqrt(3)i, where we (of course) know the answer is pi/3. You can always get it to give you a numerical answer, by typing:

float(arg(1+sqrt(3)*I))

We can even torture it into admitting that this is pi/3:

bool(float(arg(1+sqrt(3)*I))==float(pi/3))

Finding eigenvectors and eigenvalues is hard. Our general strategy was:

• Compute the characteristic polynomial. For an n x n matrix, this involves taking the determinant of an n x n matrix with entries polynomials, which is slow. (The fast method for computing determinants, row reduction, doesn’t help much since the entries are polynomials.)
• Find the roots of the characteristic polynomial. You only know a closed form formula for the case n=2. There exist formulas in terms of roots for n=3 and 4, but not for n=5 or higher. You can always approximate the roots using Newton’s method, say, but it’s at best somewhat tedious.
• For each root (eigenvalue), find the corresponding eigenvectors. This involves row reducing a matrix whose entries are perhaps complicated real numbers, once for each eigenvalue.

Fortunately, since finding eigenvalues and eigenvectors is important in practice, there are lots of techniques, and computer code for doing it, symbolically (precisely) and approximately, for general matrices and special classes.

Philosophy over; here are some commands to get started.

Before getting started, to make the output readable, type:
%typeset_mode True

Eigenvalues and eigenvectors in one step.

Let’s create the matrix from Example 5.1.4 in the text, and find its eigenvalues and eigenvectors it:
M = matrix([[4,-1,6],[2,1,6],[2,-1,8]])
M.eigenvectors_right()

Here, Sage gives us a list of triples (eigenvalue, eigenvectors forming a basis for that eigenspace, algebraic multiplicity of the eigenspace). You’re probably most interested in the first two entries at the moment. (As usual, these are column vectors even though Sage displays them as rows.)

We can test these are eigenvectors, by multiplying M by them. For example:
M*vector([1,0,-1/3])
M*vector([1,0,-1/3])==2*vector([1,0,-1/3])

If you just want the list of eigenvalues, type:
M.eigenvalues()


In M.eigenvectors_right(), The word “right” is because we want vectors v so that Mv=cv, not vM=cv. (Why don’t we have to write M.eigenvalues_right()?)

The characteristic polynomial.
M.characteristic_polynomial()

To get the roots of the characteristic polynomial, you can type:
M.characteristic_polynomial().roots()

Sage gives you pairs (root, multiplicity of that root). So, in this case, 2 occurs as a root twice, while 9 occurs once. That is, if we factor the characteristic polynomial we get:

Warning! Sage seems to define the characteristic polynomial to be det(xI – A), while the book and WebWorks use det(A-xI).

Diagonalizing
Not every matrix is diagonalizable, but every matrix has a “Jordan normal form” (which we will not discuss, alas). If the M is diagonalizable then M’s Jordan normal form is diagonal (and conversely). So, to test if M is diagonalizable, you can use:
M.jordan_form()

Alternatively, we can ask for the matrix P so that P^(-1)MP is diagonal. Sage gives this by M. The command is:
M.eigenmatrix_right()

This gives both the matrix P and P^(-1)MP. To extract just P, type:
P = M.eigenmatrix_right()[1]
P


Now we can double check:
P^(-1)*M*P

Sage’s internal help system
If you ever want documentation for a command, just type its name followed by a question mark:
M.eigenmatrix_right?

You can also get a list of possible completions by hitting tab:
M.eigen[TAB KEY]

This post’s goal is to quickly get up to speed with doing linear algebra manipulations in Sage. Work through this, typing the code into Sage. Remember to press shift-return after each piece of code.

Start by creating a new Sage worksheet.

Pretty printing
To make the matrices look nicer, type:
%typeset_mode True
and press shift-return.

Creating matrices
Creating a particular matrix is easy:
matrix([[1,2,3],[4,5,6]])
You can specify the size, though you don’t have to:
matrix(2,3,[[1,2,3],[4,5,6]])

matrix(3,3,[[1,2,3],[4,5,6]])
will generate an error (good); it’s worth getting used to what these look like.

There’s a lot of information in the error message about exactly where the error happened, but the main message is in the last line: “number of rows does not match up with specified number”.

Some particular matrices of interest are the zero matrix and the identity matrix. There’s code to create these:
identity_matrix(3)
zero_matrix(2,3)

(Here, I executed two commands at once, by hitting return after the first but shift-return after the second.)

Often you want to give matrices names:
M = matrix([[1,2,3],[4,5,6]])
I = identity_matrix(3)
This suppresses the output: when you type the above lines and press shift-return, you don’t see any output. To find out the matrices were stored, just type the names and press shift-return:
M
I

Matrix arithmetic
Matrix arithmetic works exactly as you expect, with + for matrix addition, * for matrix multiplication and ^ for matrix exponentiation (when defined); ^ is especially useful for inverses.
M = matrix([[1,2,3],[4,5,6]])
Z = zero_matrix(2,3)
I = identity_matrix(2,2)
N = matrix([[3,1],[4,1]])
N*M
Z+M
M+M
I*M
N^2
N^(-1)
M*M

(The last line should generate an error, of course, and does.)

Vectors
You create vectors with the vector command:
v = vector([1,1,1])
v
You can add vectors, multiply by scalars, and multiply by matrices:
v+v
2*v
M*v

Important. Even though the vectors look like rows, they’re really column vectors.

Row reduction
You row reduce matrices by using the “rref()” function:
M.rref()
matrix([[1,2,3],[0,1,1],[1,3,4]]).rref()

Rank and nullity
Sage computes rank and nullity:
M.rank()
M.right_nullity()

(If you just use M.nullity(), you’ll get the wrong answer: Sage prefers to think of the equation xM=b, not Mx=b, so M.nullity() is the dimension of the space of solutions to xM=0.)

Augmenting matrices
Sometimes it’s convenient to augment a matrix by a vector:
P = matrix([[1,2],[3,4]])
v = vector([-1,-2])
Q=P.augment(v)
P
v
Q

Solving systems of linear equations
Being able to augment and row-reduce is as good as being able to solve Ax=b, but maybe you prefer to have Sage give you the solution directly:
M.solve_right(vector([7,13]))
or
b = vector([7,13])
M.solve_right(b)

Let’s check it’s a solution:
x = M.solve_right(b)
M*x
M*x==vector([7,13])

If you just use M.solve, though, you will get the wrong answer. (Try it!)

Wait a moment… The nullity of M was 1, so there should be a 1-dimensional space of solutions. Sage is not giving the general solution, just one particular solution. (So, augmenting and row-reducing was better.)

What happens if there’s no solution? Try and find out.

And beyond
There’s a lot more we haven’t talked about. (For example, related to last week’s homework, Sage can find bases for null spaces and column spaces for you.) We’ve covered the most useful operations for Math 341; new Math 342 stuff next post.