Biased and unbiased estimates
Jason Wallin
(This was really little more than an excuse to get me to learn a little about Markdown in R. I have been toying with the idea of trying to move the 302 labs away from SPSS and into R. One such advantage could be the relative ease of employing simulations in R to to illustrate some of the concepts that students often report as challenging. The distinction between biased and unbiased estimates was something that students questioned me on last week, so it’s what I’ve tried to walk through here.)
In 302, we teach students that sample means provide an unbiased estimate of population means. Of course, this doesn’t mean that sample means are PERFECT estimates of population means. We should expect that the mean of any sample, no matter how representative, will differ a bit from the mean of the population from which it was drawn. This is sampling error. We say the sample mean is an unbiased estimate because it doesn’t differ systemmatically from the population mean–samples with means greater than the population mean are as likely as samples with means smaller than the population mean.
Let’s simulate this.
Creating a population
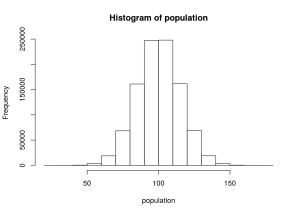
First, we need to create a population of scores. Let’s use IQ scores as an example. Here we’ll draw a million scores from a normal distribution with a mean of 100 and a standard deviation of 15. We’ll plot it as a histogram to show that everything is nice and normal.
# Define a few settings for our work today
popMean = 100; # The mean of our population
popSD = 15; # The standard deviation of our population
sampSize = 30; # The size of the samples we'll draw from the population
population <- rnorm(1000000, mean = popMean, sd = popSD)
hist(population)
Just to double check and make sure that R is doing its thing like it should, we can check some descriptive statistics for this population. If things have worked, these values should be pretty darn close to μ = 100 and σ = 15.
mean(population)## [1] 100.0175sd(population)## [1] 14.99739Yep.
Sample means are unbiased estimates of population means
Now, we need to create a sampling distribution. We will draw a sample from this population and find its mean. Then, we do that same thing over and over again a whole mess ’a times. This distribution of sample means is a sampling distribution.
Let’s give it a whirl. We’ll start with a little snippet that just gives us a single sample of 30 participants, using random sampling with replacement. When we take a peek at its mean, we should find that it is pretty darn close to 100, but with a little sampling error.
sampChamp <- sample(population, sampSize, replace=TRUE)
mean(sampChamp)## [1] 96.36024A quick aside: Just how close should it be to the population mean? Well, the expected deviation between any sample mean and the population mean is estimated by the standard error: σ2M = σ / √(n). So, in this case, we’d have a σ2M = 15 / √30 = 2.7386128
Let’s return to our simulation. We’ll now draw a whole bunch of samples and enter their means into a sampling distribution.
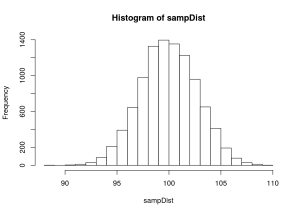
sampDist <- replicate(10000,mean(sample(population, sampSize, replace=TRUE)))
hist(sampDist)
Let’s get a few descriptive statistics here, too.
mean(sampDist)## [1] 99.96665sd(sampDist)## [1] 2.743161Note that the mean of the sampling distribution is a pretty darn good match for the original population mean. So, looky there, the sample mean is an unbaised estimator! Replications of the sampling procedure yield means that are just as likely to be above the population mean as below (in a symmetrical distribution like this, the mean and median are pretty much the same. If you’re interested, the actual value for the median is 99.950235. Also: The standard deviation of the sampling distribution is the standard error, so we see a pretty good match between the SD here (2.7431614) and the standard error calculated earlier (2.7386128).
Uncorrected sample standard deviations are biased estimates of population standard deviations
Okay, let’s put together a different sampling distribution. Rather than collecting means from each sample we’ll collect uncorrected sample standard deviations. This is the square root of the sample variance, where the sample variance is the sum of the squared deviations from the mean divided by the sample size (SS/n).
R uses the corrected sample standard devaition (and variance), by default. So I use some cheap tricks to get it to give me the uncorrected standard deviation.
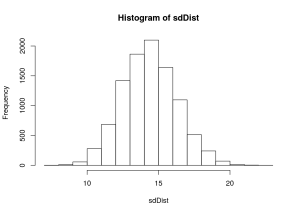
sdDist <- replicate(10000,(((sqrt(var(sample(population, sampSize, replace=TRUE)))*(sampSize-1))/(sampSize))))
hist(sdDist)
Let’s grab a mean of this sampling distribution of standard deviations.
mean(sdDist)## [1] 14.35129Notice that it is an underestimate of the population variance. The deviation between this estimate (14.3512925) and the true population standard deviation (15) is 0.6487075. Uncorrected sample standard deviations are systemmatically smaller than the population standard deviations that we intend them to estimate.
Now, let’s try it again with the corrected sample standard deviation.
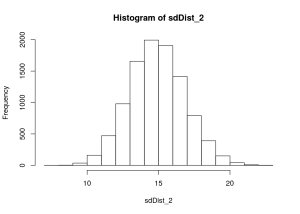
sdDist_2 <- replicate(10000,sd(sample(population, sampSize, replace=TRUE)))
hist(sdDist_2)
And its mean.
mean(sdDist_2)## [1] 14.88884Here, the deviation between the estimate from the sample(14.8888407) and the true population standard deviation (15) is reduced to 0.1111593. Sample standard deviations are less systemmatically underrepresenting the population standard deviation.